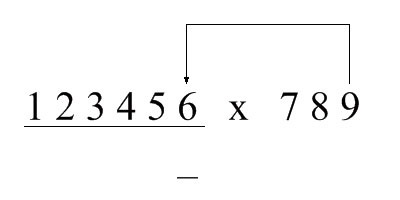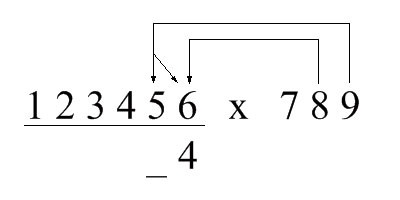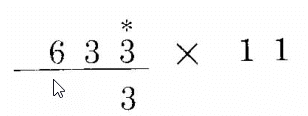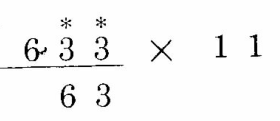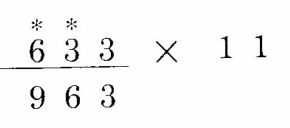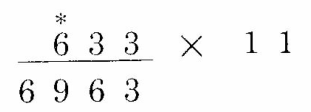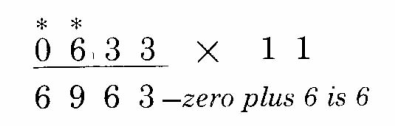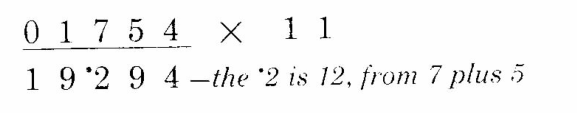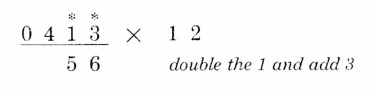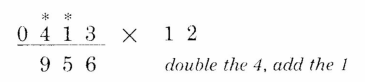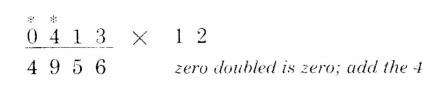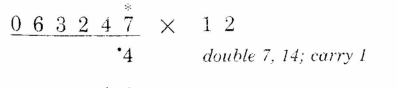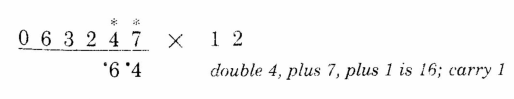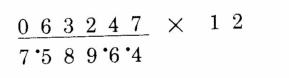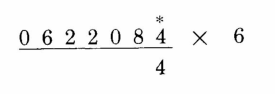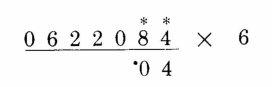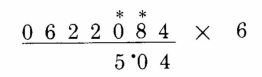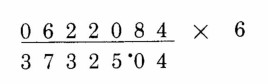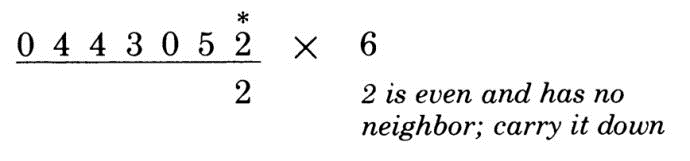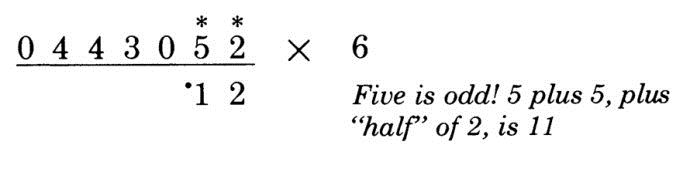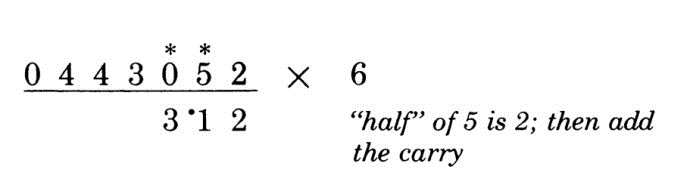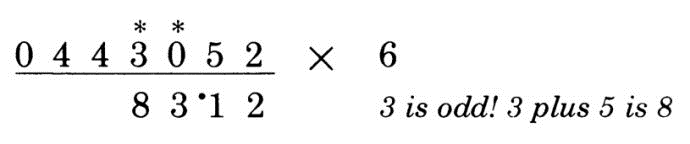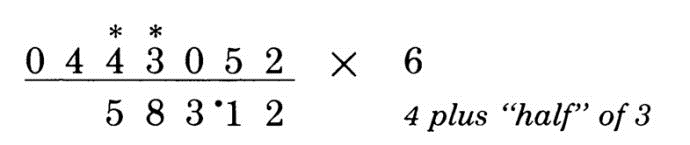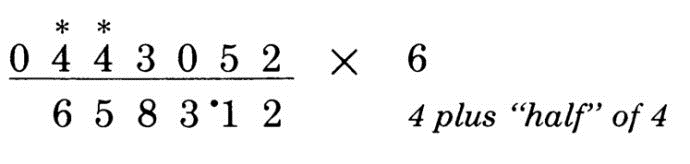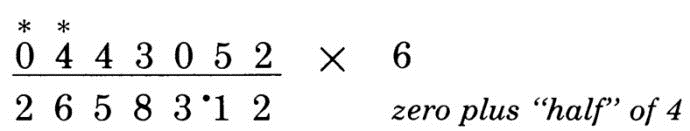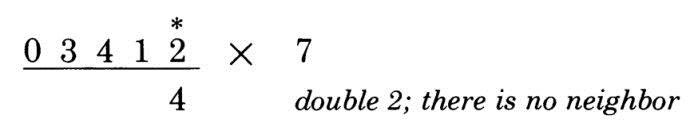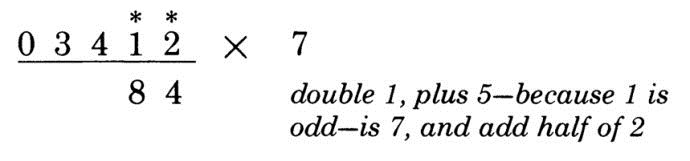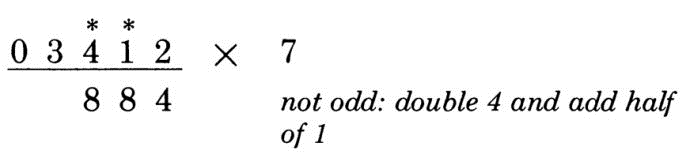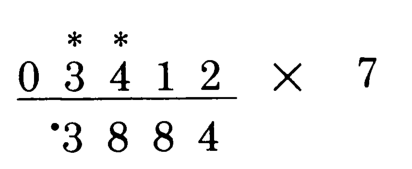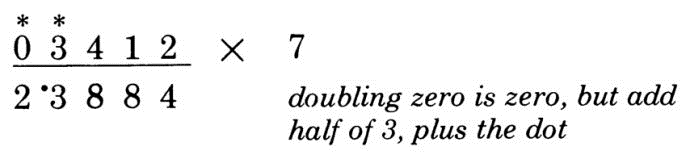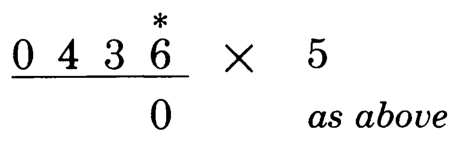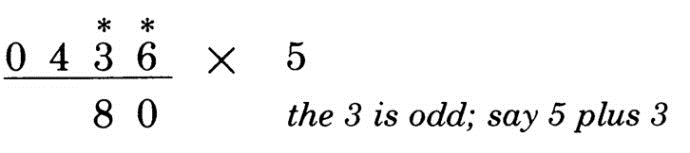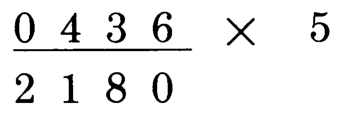二战期间,俄国的数学家Jakow Trachtenberg(1888-1953)被关进纳粹集中营,在狱中,他开发出了一套心算算法,这套算法后来被命名为Trachtenberg速算系统。
有比较才能有差别。在对比之前先来看一下我们传统教育中是怎么计算的,以乘法为例,学校里教的是酱紫的算式:
长沙seo霜天直接引用Wiki上相关介绍页面的实例, 以乘法为例,计算123456 x 789的值。
俗话说,有比较才能有差别。我们学校里教的是酱紫的算式:
再来看看Trachtenberg是怎么来算的,计算出的值从右至左分别为:
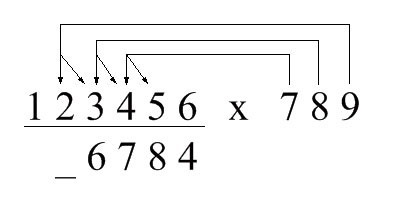
第1位(右起,下同):先算6 x 9,取个位,得到4; 来个示意图:
第2位:依次取9 x 5的个位,9 x 6的十位,
8 x 6的个位,加起来:
5 + 5 + 8 = 18
所以第2位就是8,把十位上的1带到第3位计算;示意图如下,垂直的箭头表示取这两数乘积的个位,斜的箭头则表示取乘积的十位(下同):
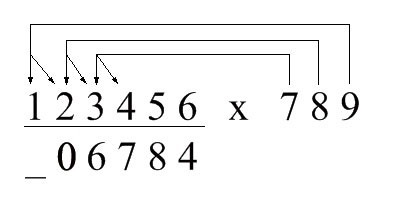
第3位:依次取9 x 4的个位,9 x 5的十位,
8 x 5的个位,8 x 6的十位,
7 x 6的个位,
以及上一步的进位(1),加起来
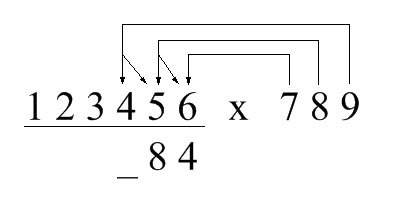
6 + 4 + 0 + 4 + 2 + 1 = 17
所以第3位是7,照例将十位上的1带到下一步计算; 示意图如下:
第4位:依次取9 x 3的个位,9 x 4的十位,
8 x 4的个位,8 x 5的十位,
7 x 5的个位,7 x 6的个位,
以及上一步的进位(1),加起来:
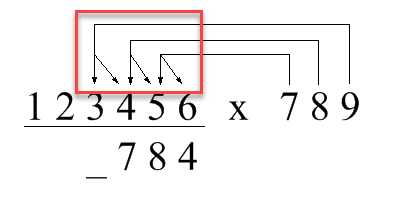
7 + 3 + 2 + 4 + 5 + 4 + 1 = 26
所以第3位是6,照例将十位上的2带到下一步计算;示意图如下:
看出点什么来了没?我们只要每次将长沙seo霜天用红线圈出的三组箭头往前移动一位,就可以知道要加哪些数。这三组箭头“可以”在计算第1位时就存在,想象一下!
所以后面几位的计算就很简单,照这个规律来就是。
第5位:
第6位:
第7位:下图中,要注意的是9 x 1的十位还是要取的,只不过该位无数值,以0代替而已;
第8位:同样,8 x 1的十位为0;
第9位:继续把箭头组往左推一位,可发现,只要计算7 x 1的十位,由于值为0,所以第9位为0,忽略。
好了,整个运算过程介绍完了。在这个计算过程中,计算者主要做了:
- 在纸横向列出算式;
- 按规则从右至左算出并写下每一位数,书写位置参考上面的示意图;
- 计算的过程很简单:会九九乘法表和简单数的相加即可;
- 心算的负担很轻,只要存住每次的进位就行,据称,这样的储存用一只手就能搞定;
这套算法不但算起来很快,而且很简单。有兴趣的童鞋可以自行通过英文版的《The Trachtenberg Speed System of Basic Mathematics》学习,这本书是Ann Cutler和Rudolph McShane编译的,详细地介绍了Trachtenberg速算系统的使用。家有适龄孩子的童鞋,学会后可以当孩子们的老师哦!
上文长沙seo霜天简单地介绍了Trachtenberg系统的乘法计算方法,针对一些特定的数字,Trachtenberg还发展出了更快的计算方法。
先来介绍乘数为11的速算方法。它的计算规则我们可称之为“邻居法则”:
从右至左,把每一位数和其右侧相邻位置的数字相加,取其个位。若所得值大于9,则将其十位则带到下一位计算(这个进位最多也只有1)。
所以以后碰到和11相乘,直接写结果就成了,举个栗子:
比如633 x 11:
第1位:右侧没数字,所以直接记作3;这里衍生出一条规则,所求值的第1位等于被乘数的第1位。
第2位:3 + 3 = 6
第3位: 6 + 3 = 9
第4位:左侧没数字了,计作0,so,0 + 6 = 6
计算的时候,也可以习惯性的也在被乘数前加个0,这个看起来更顺眼:
上面这个例子相邻两数的和没有超过9的,所以我决定再来个栗子,计算1754 x 11。当相邻两数的和大于9时,我们在写结果的时候,可以顺手在前面用一个小点标记一下,如:
第3位:7 + 5 = 12,这里的记作“.2”(相当于12), 所以要第4位就是:1 + 7 + 1 = 9。
怎么样?够简单吧?
如果你阅读过英文维基上关于Trachtenberg速算系统的介绍页面,想必你能看到Trachtenberg除了加、乘、除算法外,针对2-12这一串数字的乘法,有自己独特的算法。这些数字的乘法,Trachtenberg发现了它们的规律,而且非常简单。若能掌握,计算起来,会更加快速。
上面,长沙seo霜天已介绍过11的乘法,今天来讲12的。
12的乘法规则和11一样简单:
把被乘数的每一位乘2后再加上右邻那位的值,取其个位。若所得值大于9,则将其十位则带到下一位计算。
直接来看栗子:413 x 12
第1位(右起,下同):3 x 2 + 0 = 6. 3的右侧没数值,直接乘2即可。为方便计算,我们在被乘数的前面补个零,这样对于初学者来说,最后一位的计算不至于被轻易忽略。老手的话,直接脑补即可,以后对于前面补0的操作,不再做专门的说明。
第2位:1 x 2 + 3 = 5
第3位:4 x 2 + 1 = 9
第4位:0 x 2 + 4 = 4
怎么样?还是看到数字直接写结果,比传统的计算简单多了吧?
照例要解决“乘2加邻居”后带来的进位问题。由于这项操作最大值只有27(9 x 2 + 9),所以进位最大是2。
再来个栗子:63247 x 12
第1位:7 x 2 + 0 = 14,留下4,将1进位。还记得我们上一节讲过的前面标个小点来表示有进位的做法么?
第2位:4 x 2 + 7 = 15 + 1 = 16。留6,将1进位。
第3位:2 x 2 + 4 = 8 + 1 = 9
第4位:3 x 2 + 2 = 8
第5位:6 x 2 + 3 = 15。留5,将1进位。
第6位:0 x 2 + 6 = 6 + 1 = 7。注意此时所得的值如果大于9,则直接将进位写到下1位。
前面长沙seo霜天已讲过Trachtenberg中关于11和12的乘法,按照《The Trachtenberg Speed System of Basic Mathematics》一书的顺序,接下来我们讲5、6、7这三个数的乘法。
如果你有这本书,请翻到第28页。
先来讲6。擦,为什么要先讲6?请往下看。
6的乘法规则有两条,先讲第一条:
把被乘数的每一位加上右侧邻位的一半,保留个位,若所得值大于9,则将其十位则带到下一位计算。
这个“右侧邻位的一半”的取半操作,准确的说法是“取半求整”,就是碰到1、3、5、7、9这些奇数的时候,取其一半的整数部分。比如5的一半是2.5,我们只取2,其它依此类推。
上栗子吧:计算 622084 x 6
第1位:4 + 0 / 2 = 4
第2位:8 + 4 / 2 = 10, 取0,将1进位。
第3位:0 + 1 + 8 / 2 = 5
第4位:2 + 0 / 2 = 2
第5位:2 + 2 / 2 = 3
第6位:6 + 2 / 2 = 7
第7位:0 + 6 / 2 = 3
然而,这并不是乘6的全部规则,完整的规则是:
把被乘数的每一位加上右侧邻位的一半,如果这个数是奇数,那要先加5. 所得值保留个位。若所得值大于9,则将其十位则带到下一位计算。
直接上栗子:计算 443052 x 6
第1位:右侧没数字了,所以直接得2
第2位:注意这一位是5,要先加5,再加右侧的一半,5 + 5 + 2 / 2 = 11, 保留1, 将十位上的1进位
第3位:0 + 1 + 5 / 2 = 3。注意5 / 2的取半求整操作。另外,对有进位的情况,建议养成先加进位的习惯,如在本例中看到0,心里直接说“1”。
第4位:3是奇数,所以要先加5:3 + 5 + 0 / 2 = 8
第5位:4 + 3 / 2 = 5. 注意,在练习时要养成一个良好的习惯,不要去想“3的一半是1,4加1等于5”,做取半操作应该直接报出结果。比较理想的状况是心里想“4,5”,在刚开始练习的阶段,也可以想“4,1,5”。
第6位:4 + 4 / 2 = 6
第7位:0 + 4 / 2 = 2
看到这里,或许有童鞋会问,这和传统算法比,好像没什么优势啊?而且貌似更复杂了?
看起来是这个样子!传统算法中,是用乘法口诀将两数相乘,再处理进位。
但长沙seo霜天认为,Trachtenberg算法最大的优势是进位简单,因为最大只有一。而且相对而言,将乘法转化成了加法,亦更为简单。
此时,有吃瓜群众指出,你这特么滴还有除法,敢说简单?
亲,取半的操作辣么简单,难道你也怕?
下面请翻到35页,我们开始学习7的乘法规则。
7的乘法规则和6很相似:
把被乘数乘2后加上右侧邻位的一半,如果这个数是奇数,那要在乘2后加5。所得值保留个位。若所得值大于9,则将其十位则带到下一位计算。
我们来看栗子:计算3412 x 7
第1位:右侧没数据,所以直接乘2,得4
第2位:1是奇数,所以先乘2再加5,1 x 2 + 5 + 2 / 1 = 8
第3位:注意1取半求整后是0,4 x 2 + 1 / 2 = 8
第4位:3 x 2 + 5 + 4 / 2 = 13. 留3,将1进位。
第5位: 0 x 2 + 1 + 3 / 2 = 2,养成先加进位的习惯
最后我们来讲5的乘法规则。它有点像6和7规则的杂交版,但更简单:
取被乘数的每一位右侧邻位的一半,如果当前位是奇数,则再加5
这回连进位都不需要考虑,因为把最大的数9取半求整后是4,即使要再加5,也只能是9。
我们照例用一个栗子来理解这条规则:计算436 x 5
第1位:6是偶数,而其右侧没有数字,所以写作0.
第2位:3是奇数,5 + 6 / 2 = 8
第3位:4是偶数,所以只取 3 / 1, 得1
第4位:0是偶数,所以只取 4 / 2, 得2
总结一下就是,在5的乘法中,被乘数的每一位数只是用来判断是不是要加5,并不参与运算。 所以算起来要简单多了。