图像压缩：在本文中，我们将研究JPEG基线压缩算法…

由于图像文件通常大于文本文件，并且由于网页通常包含跨越可能较慢的连接传输的许多图像，因此有一种以紧凑格式表示图像的方法是有帮助的。在本文中，我们将看到JPEG文件如何使用可能需要的计算机存储的一小部分来表示图像。我们还将看看更新的JPEG 2000标准背后的一些数学。
这个被广泛称为数据压缩的话题提出了一个问题：“我们如何以紧凑，有效的方式来表达信息？” 除了图像文件，它是例行压缩数据，视频和音乐文件。例如，压缩使您的8吉字节iPod Nano可以容纳约2000首歌曲。我们将看到，关键是以某种方式组织信息，揭示可以消除的固有冗余。
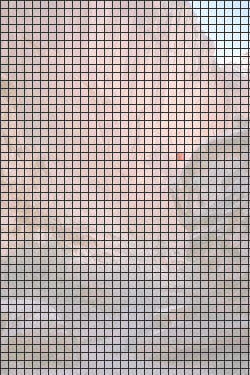
在本文中，我们将使用右侧的图像作为示例来研究JPEG基线压缩算法。（JPEG是“联合摄影专家组”的缩写。）一些压缩算法是无损的，它们保留所有原始信息。其他的，如JPEG基线算法，是有损的 – 一些信息丢失，只有被判断为微不足道的信息。
在我们开始之前，让我们天真地确定该图像需要多少计算机存储。首先，图像被排列成尺寸为250×375的矩形网格，总共具有93,750个像素。每个像素的颜色通过指定红，绿和蓝的颜色应该混合在一起多少来确定。每个颜色分量表示为0到255之间的整数，因此需要一个字节的计算机存储。因此，每个像素需要三个字节的存储空间，这意味着整个图像需要93,750X3 = 281,250字节。但是，这里显示的JPEG图像只有32,414字节。换句话说，图像已被压缩了大约九倍。

我们将描述如何在这样一个小文件（压缩）中表示图像，以及如何从该文件重构（解压缩）
JPEG压缩算法
首先，图像被分成8×8个像素块。

由于每个块都被处理而不参考其他块，所以我们将集中在一个块上。具体来说，我们将重点介绍下面突出显示的框。

这是同一块炸弹，使得各个像素更明显。请注意，8×8块（尽管其他块可能有更多）没有巨大的变化。
请记住，数据压缩的目的是以显示某些冗余的方式来表示数据。我们可以考虑由由其红，绿和蓝组成的三维向量（R，G，B）表示的每个像素的颜色 。在典型的图像中，这些组件之间存在大量的相关性。因此，我们将使用色空间变换来产生一个新的矢量，其分量代表亮度，Y和蓝色以及红色色度C _b和C _r。
亮度描述像素的亮度，而色度携带关于其色相的信息。这三个量通常与（R，G，B）组分相关性较小。此外，心理视觉实验表明，人眼对亮度比色度更敏感，这意味着我们可能忽略色度上的较大变化，而不影响我们对图像的感知。
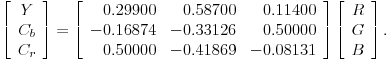
由于这种变换是可逆的，我们将能够从（Y，C _b，C _r）向量中恢复（R，G，B ）向量。当我们想重建图像时，这很重要。（确切地说，我们通常在色度分量中添加128，以便它们被表示为0到255之间的数字。）
当我们将这个变换应用到块中的每个像素时
我们获得三个新的块，一个对应于每个组件。这些显示在下面，其中较亮的像素对应于较大的值。

ÿ	C b	C r

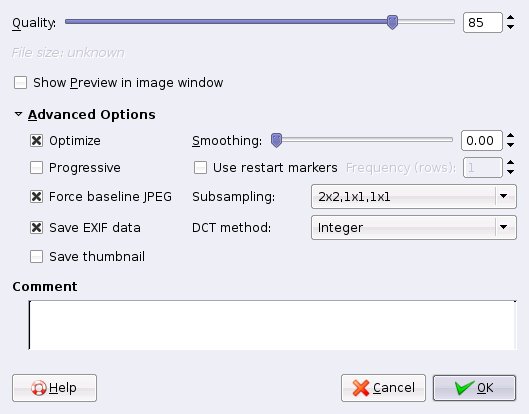
通常，亮度比色度显示更多的变化。为此，有时通过假设色度值在2乘2个块上是恒定的，从而记录更少的这些值来实现更大的压缩比。例如，当将图像保存为JPEG文件时，图像编辑软件Gimp提供以下菜单：

“Subsampling”选项允许选择对色度值进行二次采样的各种方式。另外值得注意的是“质量”参数，其重要性将很快变得清楚。

离散余弦变换

现在我们来到压缩算法的核心。我们的预期是，超过8×8的块，（Y，C _b，C _r）载体相当温和，如上面的例子所示。代替记录组件的各个值，我们可以记录平均值，以及每个像素与该平均值的差异。在许多情况下，我们预计与平均值的差异相对较小，因此可以安全地忽略。这是离散余弦变换（DCT）的本质，现在将对此进行说明。
我们首先将焦点放在我们块中的一行中的三个组件中的一个，并假设八个值由 f ₀，f ₁，…，f _7表示。我们想以这样一种方式来表示这些价值观，使变化更加明显。因此，我们将考虑由函数f _x给出的值，其中x从0到7，并将该函数写成余弦函数的线性组合：

不要担心前面的1/2的因子或常数 C _w（ 除了C ₀ = 之外的所有w，C _w = 1 ）。该表达式中重要的是函数 f _x被表示为具有系数F _w的变化频率的余弦函数的线性组合 。如下所示是四个具有相应频率w的余弦函数的曲线图。
 

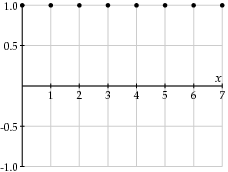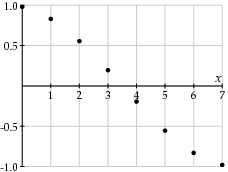w = 0	w = 1
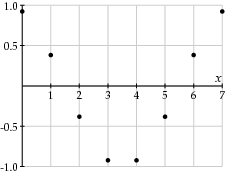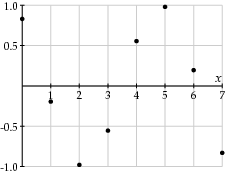w = 2	w = 3

当然，具有较高频率的余弦函数表现出更快速的变化。因此，如果值 f _x变化较慢，则较大频率的系数 F _w应该相对较小。因此，我们可以选择不记录这些系数，以减少图像的文件大小。
可以使用DCT系数

请注意，这意味着DCT是可逆的。例如，我们将从f _x开始 并记录值F _w。然而，当我们想重建图像时，我们将具有系数 F _w并重新计算f _x。
而不是将DCT应用于我们的块的行，我们将利用我们的图像的二维性质。离散余弦变换首先应用于我们块的行。如果图像在垂直方向上没有太快地改变，那么系数也不应该。因此，我们可以修正w的值， 并将离散余弦变换应用于从八行得到的F _w的八个值的收集。这导致系数F _w，u，其中w 是水平频率，u表示垂直频率。
我们将这些系数存储在另外8×8块中，如图所示：
请注意，当我们向下移动或向右移动时，我们遇到对应于较高频率的系数，我们预计这些系数不太重要。
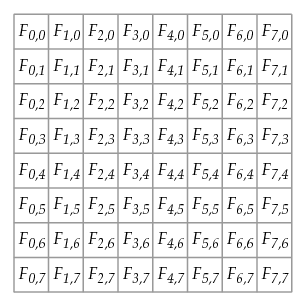
可以通过快速离散余弦变换来有效地计算DCT系数，其精神在于快速傅里叶变换有效地计算离散傅里叶变换。

量化

当然，系数F _w，u是实数，将被存储为整数。这意味着我们需要舍入系数; 正如我们将看到的，我们这样做有助于更大的压缩。而不是简单地舍入系数F _w，u，我们将首先除以 量化因子然后记录

（F _w，u / Q _w，u）这允许我们强调某些频率超过其他频率。更具体地说，人眼对图像中的快速变化不是特别敏感。这意味着我们可以通过为较高频率选择较大的量化因子，而不会对图像的视觉质量产生重大影响，而不会影响较高的频率。
还要注意，当创建一个JPEG文件时，该算法要求一个参数来控制图像的质量以及图像的压缩程度。这个我们称之为q的参数是1到100之间的整数。您应该将q视为对图像质量的度量：q的较高值 对应于较高质量的图像和较大的文件大小。从q创建 数量
以下是q的函数 图：
请注意，较高的q值会导致较低的值 。然后我们把重量作为
（F _w，u / Q _w，u）当然，通过这个四舍五入的过程将会丢失信息。当任何一个或 Q _w，u增加（记住对应于质量参数q的较小值的大值），更多信息丢失，并且文件大小减小。
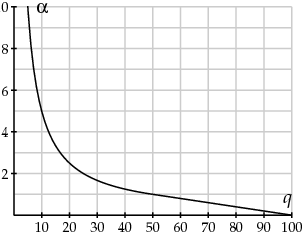
以下是JPEG标准推荐的Q _w的典型值。首先，对于亮度系数：
并且对于色度系数：
选择这些值以强调较低的频率。我们来看看我们的例子如何运作。请记住，我们有以下值的值：
 

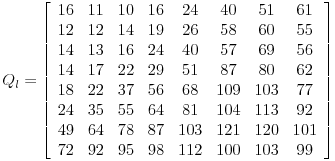
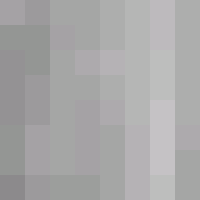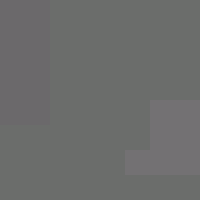ÿ	C b	C r

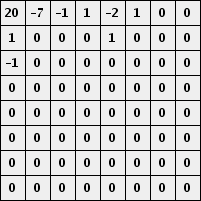
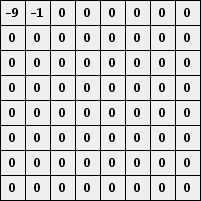
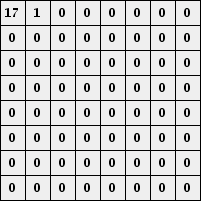
使用q = 50进行量化给出以下块：
 

ÿ	C b	C r

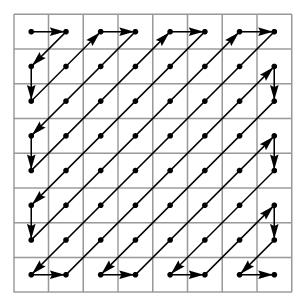
左上角的条目基本上代表块的平均值。向右移动增加水平频率同时向下移动增加垂直频率。这里重要的是有很多零。我们现在按如下所示排列系数，使得较低的频率首先出现。

特别地，对于我们记录的亮度系数
20 -7 1 -1 0 -1 1 0 0 0 0 0 0 0 -2 1 1 0 0 0 0 … 0而不是记录所有的零，我们可以简单地说出有多少出现（注意在色度权重中还有更多的零）。以这种方式，DCT系数的序列大大缩短，这是压缩算法的目标。事实上，JPEG算法使用非常有效的手段来编码这样的序列。
当我们重构DCT系数时，我们发现
 

原版的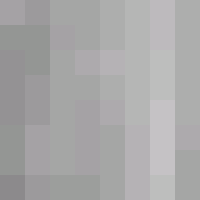
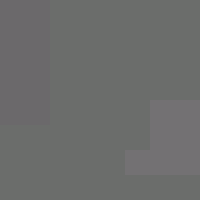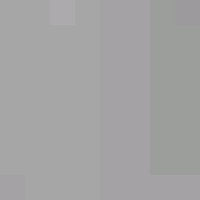重建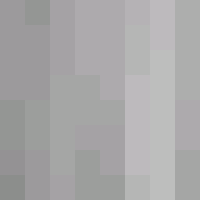
	ÿ	C b	C r

从信息重建图像是相当简单的。量化矩阵被存储在文件中，使得可以重新计算DCT系数的近似值。从这里，通过逆离散余弦变换找到（Y，C _b，C _r）向量。然后通过反转颜色空间变换来恢复（R，G，B）向量。
这是8到8块的重建，参数q设置为50

原版的	重建（q = 50）

以下，质量参数q设置为10.如预期的那样，参数q的较高值给出更高质量的图像。

原版的	重建（q = 10）

JPEG 2000

虽然JPEG压缩算法已经相当成功，但有几个因素造成了一种新算法的需要，其中有两个我们将要描述。
首先，JPEG算法对DCT的使用导致8×8块的边界处的不连续性。例如，块的边缘上的像素的颜色可以受到块中任何位置的像素的颜色的影响，而不受另一块中的相邻像素的影响。这导致了由质量参数q设置为5 创建的图像版本所示的 阻塞伪像（顺便说一下，此图像文件的大小只有1702字节），并解释了为什么JPEG不是存储线条艺术的理想格式。

此外，JPEG算法允许我们仅在一个分辨率下恢复图像。在某些情况下，也希望以较低分辨率恢复图像，例如允许在下载完整图像时以逐渐更高的分辨率显示图像。
为了满足这些要求，2000年12月引入了JPEG 2000标准。虽然两种算法之间存在一些差异，但我们将集中注意JPEG 2000使用小波变换代替DCT。
在我们解释JPEG 2000中使用的小波变换之前，我们将考虑一个更简单的小波变换示例。像以前一样，我们可以想像，我们正在处理每个像素的亮度 – 色度值。DCT通过将变换应用到一行一次，然后转换列。小波变换将以类似的方式工作。
为此，我们假设我们有一个序列f ₀，f ₁，…，f _n描述一行像素中三个分量之一的值。像以前一样，我们希望将序列中的快速变化与较慢的变化分开。为此，我们创建一个小波系数序列：
请注意，偶数系数记录两个连续值的平均值 – 由于关于高频变化的信息丢失，我们将其称为低通频带 – 而奇数系数记录两个连续值的差值 – 我们称之为高通频带作为高频信息传递。低通系数的数量是原始序列中数值的一半（高通系数的数量）。
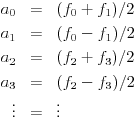
重要的是要注意，我们可以从小波系数中恢复原来的 f值，就像在重构图像时需要做的那样：
我们通过列出低通系数，然后列出高通系数来重新排序小波系数。与二维DCT一样，我们现在可以应用相同的操作来垂直变换小波系数。这导致通过低通和高通带将小波系数的二维网格划分为四个块：
像以前一样，我们使用人眼对快速变化不那么敏感，以通过与JPEG算法中所看到的量化过程相反的量化过程来强调高通系数所看到的快速变化。注意，LL区域是通过对2×2块的值进行平均而得到的，因此表示图像的较低分辨率版本。
在实践中，我们的形象被分解成瓦片，通常尺寸为64乘64。选择权力2的原因很快就会显现出来。我们将演示使用我们的图像与指示的瓷砖。（这个图块是128×128，这样可以在这个页面上更容易看到。）
注意，如果我们首先在LL区域中传输系数，则可以在所有系数到达之前以较低的分辨率重建图像，这是JPEG 2000算法的目的之一。
我们现在可以对LL区域中的较低分辨率图像执行相同的操作，从而获得较低和较低分辨率的图像。
小波系数可以通过 如下这样的提升过程来计算：
的优点是，该系数可以在不使用额外memory–计算机来计算一个₀第一替换 ˚F ₀，然后一个₁替换 ˚F ₁。此外，在JPEG 2000算法中使用的小波变换中，提升过程可以更快地计算系数。

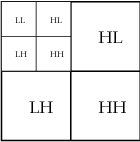
JPEG 2000小波变换

上述小波变换虽然在精神上类似，但比JPEG 2000标准中提出的更简单。例如，期望在超过两个连续值上平均以获得重建图像中的更大的连续性，并且因此避免诸如块状伪像之类的现象。所使用的小波变换之一是Le Gall（5,3）样条，其中低通（偶数）和高通（奇数）系数由

如前所述，这种变换是可逆的，并且有一个提升方案来有效地执行它。标准中包含的另一个小波变换是Cohen-Daubechies-Fauraue 9/7双正交变换，其细节稍微复杂一点，虽然描述了一个简单的提升配方来实现它。
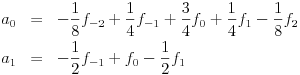
比较JPEG和JPEG 2000是值得的。一般来说，这两种算法具有相似的压缩比，尽管JPEG 2000需要更多的计算量来重构图像。JPEG 2000图像在高压缩率下不显示JPEG图像中存在的块伪影，而是随着压缩增加而变得更加模糊。JPEG 2000图像通常由人类判断为具有更高的质量。
目前，JPEG 2000并不被网络浏览器广泛支持，而是用于数码相机和医学影像。还有一个相关标准，Motion JPEG 2000，用于数字电影行业。

参考

• JPEG委员会 和 JPEG 2000委员会的主页
• Tinku Archarya，Ping-Sing Tsai， JPEG2000 Standard for Image Compression：Concepts，Algorithms and VLSI Architectures， Wiley，Hoboken。2005年。
• 金立， 图像压缩：JPEG 2000的数学，现代信号处理，第46卷，2003年。
• Ingrid Daubechies， 十节小波讲座， SIAM，费城。1992年。
• KR Rao，Patrick Yip， Discrete Cosine Transform：Algorithms，Advantage，Applications， Academic Press，San Diego。1990年。
• JPEG和 JPEG 2000的维基百科条目 。